T12：滑动窗口求和

---

完整程序

import random
c = [1,1,1,1,2,3,2,3,2,3] + [random.randint(1,9) for i in range(80)] + [2,3,2,2,2,2,1,1,1,1]

qa=[0,0,0,0,0]
qb=[0,0,0,0,0]
h,t=0,4
temp = 0
for k in range(100):
    qa[t]=c[k]
    qb[t]=temp+qa[t]-qa[h]
    print(qb[h],qb[t])
    temp=qb[t]
    t=(t+1)%5
    h=(h+1)%5

---

模拟法

在考场中很多人可能会被中间的80个随机数吓到，但显然这题不是让你去把80个数全写出来模拟一遍

qa,qb每5次循环就会被完全更新一遍，那么从第91次循环开始的h,t的位置和第1次完全相同

而且80个数是被略去的，说明中间的数必定和答案无关

因此，我们可以把前面的结果全部当作0，从最后10个数字开始写：

为方便阅读，qa[h] qb[h]用粗体标注，qa[t] qb[t]用斜体标注

注意：考场上没时间列表，可以把两个数组写出来并通过划掉原先数字的方法更新数组

qa	qb
0,0,0,0,2	0,0,0,0,2
3,0,0,0,2	5,0,0,0,2
3,2,0,0,2	5,7,0,0,2
3,2,2,0,2	5,7,9,0,2
3,2,2,2,2	5,7,9,9,2
3,2,2,2,2	5,7,9,9,8
1,2,2,2,2	7,7,9,9,8
1,1,2,2,2	7,6,9,9,8
1,1,1,2,2	7,6,5,9,8
1,1,1,1,2	7,6,5,4,8

由此可见，qb[h]为8，qb[t]为4

故选择B项。

原理：滑动窗口的求和

前面的方法简单粗暴，但在紧张的高考考场上这样做浪费时间且搞人心态（本人就是模拟出不存在选项导致心态炸裂的）

现在我们从程序出发看看它的原理

---

从t=(t+1)%5和h=(h+1)%5可以看出，qa和qb是循环队列，而h和t是队列的头和尾，队列长度始终为4

现在来看对qa和qb操作的部分，这三句是题目的精髓所在：

qa[t]=c[k] #进入循环的第一件事，将c[k]中读到的内容入qa队
qb[t]=temp+qa[t]-qa[h] 
temp=qb[t] #将计算的结果存入临时变量temp

重点来看qb[t]=temp+qa[t]-qa[h]。temp是上次操作的结果，它被加上了qa[t]并减去了qa[h]，而qa[t]与c[k]相等

那么这行代码相当于:本次结果=上次结果+c[k]-qa[h]，如果忽略掉减去的qa[h]，是不是有点累加的感觉了？在循环中，c[k]被加上并进入循环队列

当循环队列被填满时，最先进入的数字(qa[h])就被减去并出队

这就相当于在c上长度为4的一个滑动窗口。每做一次循环，窗口向前移一个单位，并将窗口中数字和存储于qb中。代码通过在每次迭代中加上新元素、减去旧元素，实现窗口和的更新

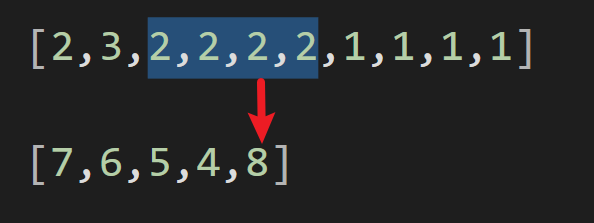
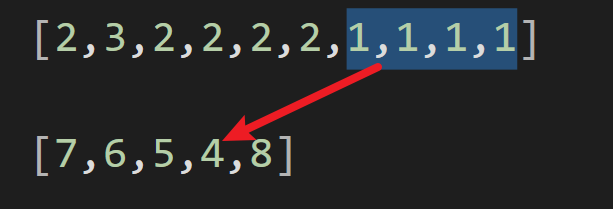
倒数第五次的窗口和(8)和最后一次的窗口和(4)就是最终答案

这也印证了可无视随机数的原因：中间的随机数在当前窗口之外，其影响在计算过程中被抵消，不会影响最后一行的输出结果